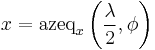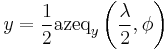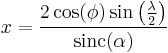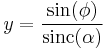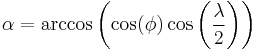Aitoff projection
The Aitoff projection is a modified azimuthal map projection. Proposed by David A. Aitoff in 1889, it is the equatorial form of the azimuthal equidistant projection, but stretched into a 2:1 ellipse while halving the longitude from the central meridian:
where 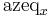 and
and 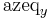 are the x and y components of the equatorial azimuthal equidistant projection. Written out explicitly, the projection is:
are the x and y components of the equatorial azimuthal equidistant projection. Written out explicitly, the projection is:
where
and 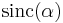 is the unnormalized sinc function with the discontinuity removed. In all of these formulas,
is the unnormalized sinc function with the discontinuity removed. In all of these formulas,  is the longitude from the central meridian and
is the longitude from the central meridian and  is the latitude.
is the latitude.
Three years later, Ernst Hermann Heinrich Hammer suggested the use of the Lambert azimuthal equal-area projection in the same manner as Aitoff, producing the Hammer projection. While Hammer was careful to cite Aitoff, there has been some confusion since, wherein Aitoff has been attributed to Hammer's projection.[1]
See also
References
- ^ Flattening the Earth: Two Thousand Years of Map Projections, John P. Snyder, 1993, pp.130-133, ISBN 0-226-76747-7.